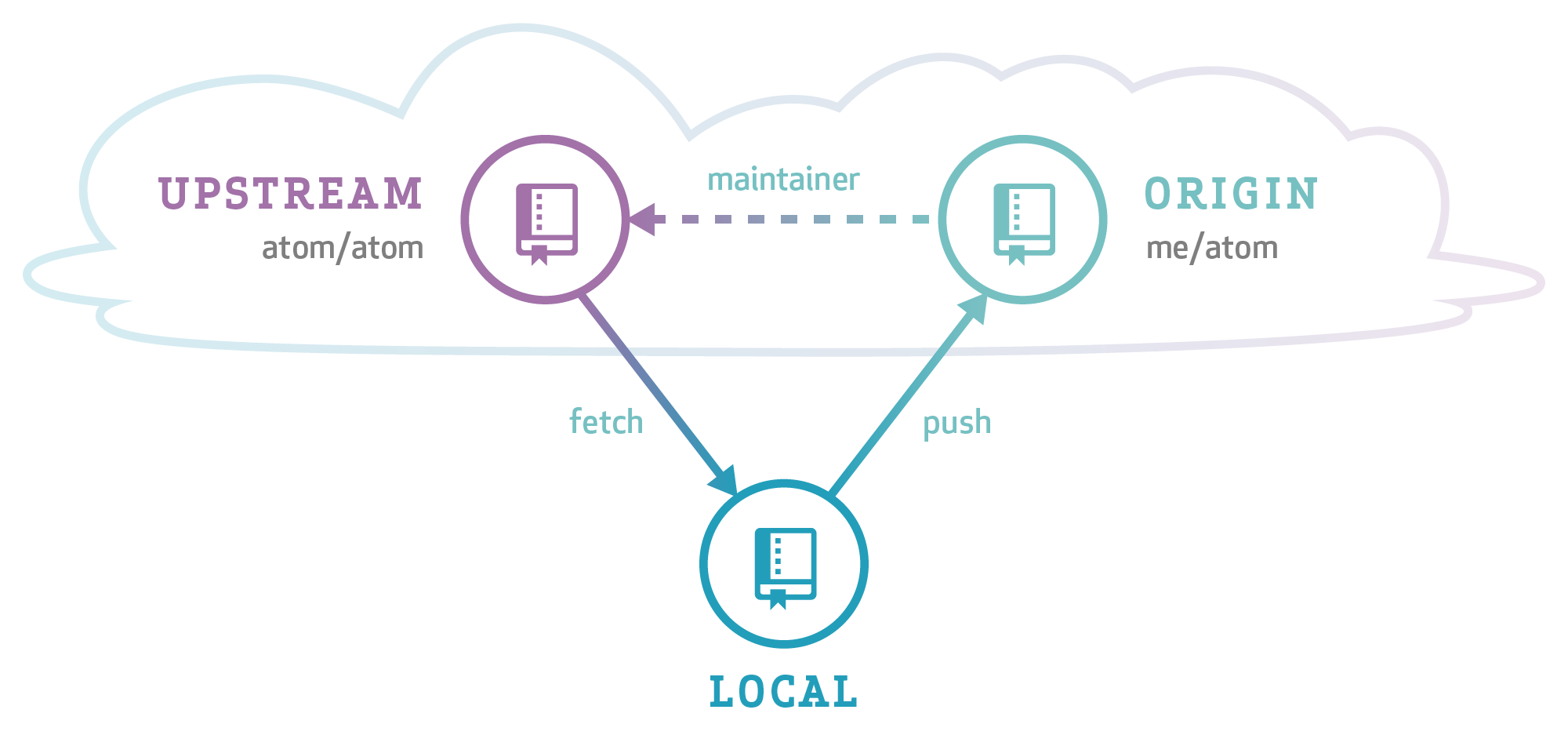
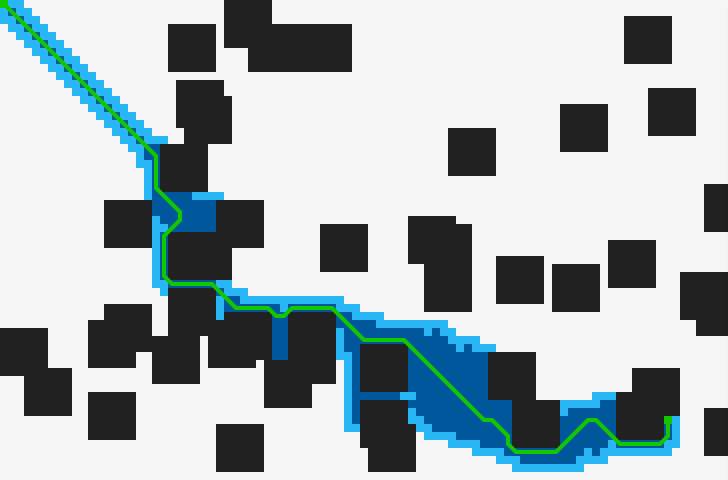
A* is a static path search algorithm which is used to find the shortest path from the source (S) to the goal (G) from a finite weighted graph. The math representation of A* is
$$f(n) = c(n) + h(n) $$
Some people may prefer using $g$ instead of $c$ to indicate the cost function. And the $h$ is a heuristic function. More information can be found from the original paper.
So let’s get back to the title, how about the admissibility of A*? Well, as we can guess, it actually relies on the heuristic function. Again, A* algorithm requires the $h$ should be a ‘good’ estimation or ‘admissible’. It means that it has to be no longer than the actual distance. But if $h$ has no meaning, e.g. 0, then it is BFS. An example in real life is letting $h$ be the Euclidean distance from the node to the goal in navigation. But what does it do with the optimality? Here’s a simplified math proof – proof by contradiction:
Say all previous states till $n$ have optimal cost values already. For the next state till $n’$ we would have $f(n’)=c(n’)+h(n’)$ which is minimum among states in OPEN list. But let’s assume $g(n’)$ itself is actually suboptimal, that means there has to be at least one state $n’^*$ on an optimal path from S that is in OPEN,
$$c(n’^*) + h(n’^*) \geq c(n’) + h(n’) \qquad (1)(\text{min})$$
meaning on the same time we have
$$c(n’^*) + \delta(n’^*, n’) < c(n’) \qquad (2)(\text{assumption})$$
Rewrite (2) can give us
$$c(n’^*) + \delta(n’^*, n’) + h(n’) < c(n’) + h(n’) \qquad (3) $$
As $h$ is admissible, we have
$$h(n’^*) + \delta(n’^*, n’) < h(n’) \qquad (4) (
\text{underestimate}) $$
So (3) would be
$$ c(n’^*) + h(n’^*) < c(n’) + h(n’)$$
which is contradictory with (1), so $c(n)$ must be optimal.